A naive autoencoder on FashionMNIST

Today we'll recreate the fastai notebook on autoencoders, where we train a vanilla autoencoder in FashionMNIST. Even though the autoencoder was actually doing a pretty bad job, it will be good practice for working with HuggingFace databases, CNNs and autoencoders.

Getting the data

import datasets
from torch.utils.data import Dataset, DataLoader

ds_name = ("zalando-datasets/fashion_mnist")
ds = datasets.load_dataset(ds_name)
ds

DatasetDict({
    train: Dataset({
        features: ['image', 'label'],
        num_rows: 60000
    })
    test: Dataset({
        features: ['image', 'label'],
        num_rows: 10000
    })
})

Trying to instantiate a dataloader raises an exception

dl = DataLoader(ds['train'], 4, shuffle=True)

 TypeError: default_collate: batch must contain tensors, numpy arrays, numbers, dicts or lists; found <class 'PIL.PngImagePlugin.PngImageFile'>

We need to convert the data which is currently a PIL image to tensors. We can do this with a collate function, which can be passed to DataLoader as the arg collate_fn

To figure out what I the collate function gets the hacky way (reading docs suckzzz), I wrote it as follows

def collate_f(*args):
  import pdb; pdb.set_trace()

which opens pdb. We can then call args and see what we got, which is one argument:

[{'image': <PIL.PngImagePlugin.PngImageFile image mode=L size=28x28 at 0x7F3233E4B320>, 'label': 6},
 {'image': <PIL.PngImagePlugin.PngImageFile image mode=L size=28x28 at 0x7F3233E49C40>, 'label': 3},
 {'image': <PIL.PngImagePlugin.PngImageFile image mode=L size=28x28 at 0x7F3233E4B470>, 'label': 3},
 {'image': <PIL.PngImagePlugin.PngImageFile image mode=L size=28x28 at 0x7F3233E4B3E0>, 'label': 0}]

We get back a list of dicts, each dict has an 'image' and 'label' keys, so what we'll do is collate the images to one tensor and the labels to another tensor. Of course, we also need to convert the PIL images to tensors.

from operator import itemgetter
from torch import tensor
import torchvision.transforms.functional as TF

ig = itemgetter('image', 'label')

def collate_f(b):
  imgs, labels = zip(*map(ig, b))
  return torch.stack([TF.to_tensor(im) for im in imgs]), tensor(labels)

Lots happening here, I invite you to copy the code to a jupyter notebook and check it out.

Model

We'll use a pure convolutional network. As a start we'll do classification, so we'll need to downsample to get to the right shape of 10 elements.

import torch.nn as nn

def conv(in_c, out_c, k=3, stride=2, act=True):
  padding = k // 2
  ret = nn.Conv2d(in_c, out_c, k, stride, 1)
  if act:
    ret = nn.Sequential(ret, nn.ReLU())
  return ret

model = nn.Sequential(
  conv(1, 4), # 14x14
  conv(4, 8), # 7x7
  conv(8, 16), # 4x4
  conv(16, 16), # 2x2
  conv(16, 10, act=False), # 1x1
  nn.Flatten()
)
x, y = next(iter(dl))
model(x).shape

torch.Size([4, 10])

The stride=2 parameters basically downsamples the image. Also notice that we don't use relu in the last layer, as we allow the logits to be negative. Let's fit!

epochs = 5
bs = 256
lr = 4e-1
dl = DataLoader(ds['train'], bs, shuffle=True, collate_fn=collate_f, num_workers=8)
opt = optim.SGD(model.parameters(), lr)


for e in range(epochs):
  model.train()
  for i, (x, y) in enumerate(dl):
    x, y = x.cuda(), y.cuda()
    opt.zero_grad()
    y_pred = model(x)
    loss = F.cross_entropy(y_pred, y)
    loss.backward()
    opt.step()
  model.eval()
  val_acc, val_loss = metrics(model, ds['test'])
  print(f"{e}: acc={val_acc:.2f} loss={val_loss:.2f}")

Running this prints

0: acc=0.38 loss=1.76
1: acc=0.73 loss=0.71
2: acc=0.78 loss=0.62
3: acc=0.82 loss=0.48
4: acc=0.82 loss=0.57

Note: I spent some time here. First I had negative loss and things didn't work, but I realized I used F.nll_loss which expects normalized logits, unlike F.cross_entropy which jibes with unnormalized logits. Then I thought I was getting much worse results compared to the notebook, but I realized my comparison was to MNIST performance, which must be easier than FashionMNIST. Still, we get a bit worse results, in the notebook they get 0.87 accuracy.

Classification works fine, let's move on to to auto-encoding. For that we need to use deconvolution, which upscales the activations. It is done by combining nearest neighbor upscale and a convolution which doesn't reduce dimensions.

ae = nn.Sequential(
  conv(1, 4), # 14x14
  conv(4, 8), # 7x7
  conv(8, 16), # 4x4
  nn.Upsample((7,7)),
  conv(16, 8, stride=1),
  nn.Upsample((14,14)),
  conv(8, 4, stride=1),
  nn.Upsample((28,28)),
  conv(4, 1, stride=1),
).cuda()
ae(x).shape

torch.Size([96, 1, 28, 28])

The training loop should be pretty similar, except now we don't care about the labels

epochs = 500
bs = 16
lr = 2e-3
dl = DataLoader(ds['train'], bs, shuffle=True, collate_fn=collate_f, num_workers=8)
opt = optim.SGD(model.parameters(), lr)


for e in range(epochs):
  for i, (x, y) in enumerate(dl):
      x = x.cuda()
      opt.zero_grad()
      x_hat = ae(x)
      loss = F.mse_loss(x_hat, x)
      loss.backward()
      opt.step()
      if i % (len(ds['train']) // (bs *10)) == 0:
        print(f"loss={float(loss):.2f}")

Training doesn't seem to be going well. As an experiment I try to fit only on the first batch, but the loss is stuck as 0.30 (the image is between 0-1) so that pretty high. I recall now that the last layer was a sigmoid activation, let's add it and see what's up.

We can look at the histogram of the pixel values of one image and it's reconstruction.

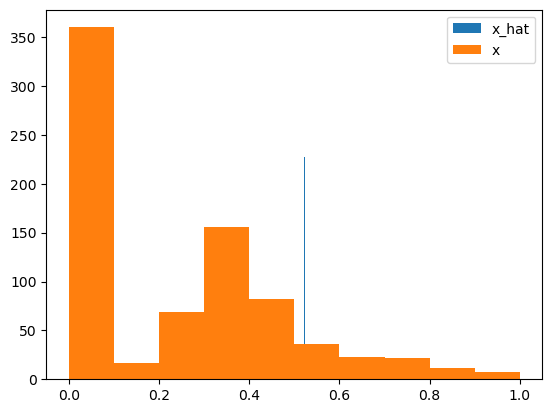
We see that the reconstruction is really bad, for some reason it's all centered at 0.5 which means pre-activations are close to 0.

Well, turns out it was mostly a bug, as you can see above the optimizer was initialized to track the previous model's parameters... fixed it to

opt = optim.SGD(ae.parameters(), lr)

Still, there wasn't immediately an improvement. Comparing to the notebook, the model pads the input image to be a power of 2, and downsamples only down to 8x8. They also used UpsamplingNearest2d but I think it does the same thing as Upsample

ae = nn.Sequential(
  nn.ZeroPad2d(2),
  conv(1, 4), # 16x16
  conv(4, 8), # 8x8
  nn.UpsamplingNearest2d(scale_factor=2),
  conv(8, 4, stride=1),
  nn.UpsamplingNearest2d(scale_factor=2),
  conv(4, 1, stride=1, act=False),
  nn.ZeroPad2d(-2),
  nn.Sigmoid(),
).cuda()

at first I still had the "model collapse" phenomena but now I can't reproduce it. Anyway, after a few epochs the loss stabilizes on 0.02 and we get this type of reconstruction:

It's very blurry, it seems like the model has a hard time reconstructing details. I wonder how we will solve this in the next lessons.

Getting the data

Model

social