AoC is back for another year! This time it's a bit shorter, only 12 days. This might be a good change overall, since in 2023 I fizzled out around day 20.

The first day has us simulating a dial ranging from 0 to 99 on a safe, where we needed to repeat a list of rotation instructions (left/right + number of clicks). Part 1 asked how many times the dial ended up on 0 after completing each instruction. Part 2 complicated this by also counting every time the dial crossed 0 during a rotation — so a single 200-click rotation clockwise would cross 0 twice. Both parts required fairly straightforward modular arithmetic, and I solved it in Python using a Jupyter notebook.

For day 2, I decided to solve today's problem using typescript. I programmed a lot in it in the last year on the job and I actually kind of like the language, but because we were very AI development-driven I didn't get to actually write much code myself, instead mostly prompting and reading. This robbed me of the fingertips automaticity I have in python. I don't know what the future entails for programming, but for now, creating a ts file and not even remembering the for-loop syntax feels a little humbling.

Here's what I did then: I opened Claude Code side-by-side and instructed it to be a tutor and not make any code changes. This allowed me to get relevant answers to tech questions (syntax etc) quickly while still writing stuff manually. I think I'll also add some flashcards for the syntax (though I'm still a little ambivalent about it, boring flashcards are a net negative).

The problem was to parse a list of number ranges (11-22,33-100 etc) and sum all the 'doubled' numbers in those ranges — ie numbers of the form 123123, 3333, 11. Alright, bruteforce and stringifying solved it well enough. In fact, most of the time was spent on learning how to do ts dev with nvim (I love new toys), how to read the exceptions, and looking up silly syntax stuff (how to do floor division, Math.floor(a / b)).

The second part generalized this: sum any periodic number, like 111, 123123123, 1414 etc. I had a tingling sensation, and then it came to me: I actually solved something similar at work! we had a problem where we had Gemini do OCR to pdfs, and it would sometimes go bonkers and generate really long repeating strings. We wanted to detect that. This was almost the same problem, except in our case, it was harder, because we were looking for a periodic substring. So how did I solve it? I couldn't recall... and why was that? because it was vibecoded!!!

Yep, it came back to bite me. I even remember putting time to understand how it solved it, after all it was my responsibility, and I did understand it at the time. And still, a few months later, I couldn't recall how it worked. Maybe I shouldn't be too harsh with myself, after all, I did remember that I had this problem, and maybe it's a responsible decision not to spend a lot of time on a math/algo problem in my fullstack startup job which requires to move fast bla bla bla. Nevertheless, here we were.

Anyway, after reading the code I figured it was probably not the right approach, and set out to solve it myself. The naive solution came to mind immediately:

• iterate on all the numbers in the ranges
• for each number, iterate on all possible periods (p can be a period if it divides the number of digits)
• for each period, check that n[i] == n[i+p] for all appropriate i.

Depending on the size of the ranges this approach could be good enough. But was there something better? I always look for the math angle. I remembered some leetcode problem which sounded similar, where given two strings s1 and s2 you need to decide if they are both periodic with the same pattern. The solution is to concatenate them twice, s1s2 and s2s1 and check for equality, as this is equivalent. Still, in our case this didn't help.

Then I had a whole deep think about how we can represent these numbers as a tuple (pattern, n_periods). Maybe we can simply iterate on the periodic numbers in order, ie generating instead of verifying. I thought long and hard, and had claude generate this artifact:

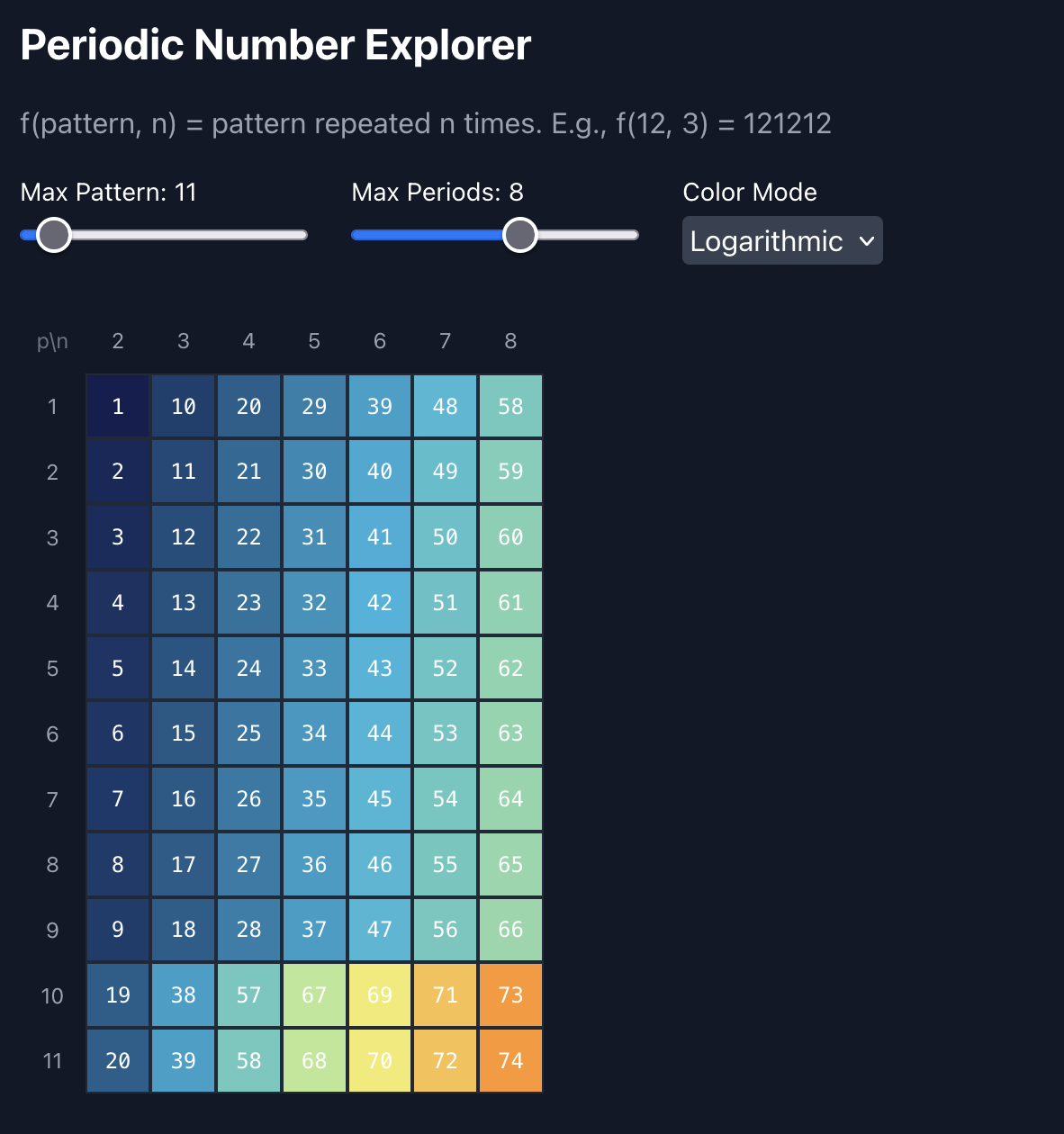
You can see that the order (the numbers inside the tiles) is a little bit tricky to figure out. I thought about the different cases, and I got to something that looked reasonable, but a feeling of tiredness came over me and I decided to write the naive solution. Surprisingly, it took very little time and was correct, and so the second day was done.

I looked online at solutions and everyone seemed to converge on the bruteforce approach. I asked claude if it can think of something better, and it came up with my suggestion, to generate the periodics instead of verifying. I had it write up a solution, and to my snarky enjoyment, it fell into the pitfalls I anticipated - namely, that two tuples can represent the same number (consider (1, 4) and (11, 2)). I pointed it out, it corrected, but still it was way off in terms of the result. At that point I intervened and explained my approach (to do it serially) and it got excited. I gave it the pointers, and it went ahead and implemented it with one mistake, quickly corrected, and voilà, we got the same result with a 100x speedup. Pretty dope. Btw, here's the solution à la Claude.

Optimized Solution Approach:

• Core idea: Iterate through valid periodic numbers directly instead of testing every number in the range
• Key function: nextPeriodic(n) computes the next periodic number after n by considering a small set of candidates:
• Same length: For each valid period p dividing n.length, try pattern n.slice(0,p) or n.slice(0,p)+1
• Next length: Use largest period dividing the new length with pattern 10^(period-1) (e.g., 999 → 1010, not 1111)
• Algorithm: Start at first periodic in range, then repeatedly call nextPeriodic() until exceeding range end
• Performance: Reduces from checking ~27M candidates to generating only ~32 valid numbers
• Result: ~95x speedup by transforming O(range_size) brute force into O(number_of_solutions) iteration

I wouldn't completely trust the big-O analysis, but other than that pretty good explanation.

Here's the final code:

import fs from 'fs';

const input = fs.readFileSync("2/input.txt", 'utf-8');

function process(input: string): number[][] {
    return input.split(",")
        .map(t => t.split('-'))
        .map(([a, b]) => [parseInt(a), parseInt(b)]);
}

function isPeriodic(n: number): boolean {
    const s = n.toString();
    for (let p = 1; p <= s.length / 2; p++) {
        if (s.length % p !== 0) continue;
        let valid = true;
        for (let i = 0; i < s.length - p; i++) {
            if (s[i] !== s[i + p]) {
                valid = false;
                break;
            }
        }
        if (valid) return true;
    }
    return false;
}

// Generate periodic number from pattern and repetitions
function makePeriodicNumber(pattern: string, reps: number): number {
    return parseInt(pattern.repeat(reps));
}

// Find first periodic number of given length
function firstPeriodicOfLength(len: number): number {
    // Find LARGEST period that divides len (gives smallest number)
    for (let period = Math.floor(len / 2); period >= 1; period--) {
        if (len % period === 0) {
            const pattern = '1' + '0'.repeat(period - 1);
            return makePeriodicNumber(pattern, len / period);
        }
    }
    return -1;
}

// Find next periodic number after n
function nextPeriodic(n: number): number {
    const s = n.toString();
    const len = s.length;
    const candidates: number[] = [];

    // Case 1: Next length (always the minimal periodic of that length)
    candidates.push(firstPeriodicOfLength(len + 1));

    // Case 2: Same length - try all possible periods
    for (let period = 1; period <= len / 2; period++) {
        if (len % period !== 0) continue;
        const reps = len / period;

        const pattern = s.slice(0, period);
        const patternNum = parseInt(pattern);

        // Try current pattern
        const samePattern = makePeriodicNumber(pattern, reps);
        if (samePattern > n) {
            candidates.push(samePattern);
        }

        // Try pattern + 1 (if it doesn't overflow)
        const nextPattern = (patternNum + 1).toString();
        if (nextPattern.length === period) {
            const nextCandidate = makePeriodicNumber(nextPattern, reps);
            if (nextCandidate > n) {
                candidates.push(nextCandidate);
            }
        }
    }

    return Math.min(...candidates.filter(c => !isNaN(c)));
}

// Optimized version
function twoOptimized(input: string) {
    const ranges = process(input);
    let sum = 0;

    ranges.forEach(([a, b]) => {
        // Start at a if it's periodic, otherwise find next periodic after a
        let current = isPeriodic(a) ? a : nextPeriodic(a);
        while (current <= b) {
            sum += current;
            current = nextPeriodic(current);
        }
    });

    return sum;
}

// Brute force for comparison
function twoBruteForce(input: string) {
    const ranges = process(input);
    let sum = 0;
    ranges.forEach(([a, b]) => {
        for (let i = a; i <= b; i++) {
            if (isPeriodic(i)) {
                sum += i;
            }
        }
    });
    return sum;
}

After wrapping everything up and deciding to write a blog post, I of course immediately said to myself "why didn't you write it on the go, this would have made it less of a hassle". The next option that came to mind was to write a literate jupyter notebook (i've been looking at solveit recently) but that's for python. Or is it? quick google AI search told me there's a deno kernel which I installed. That solves two problems, the aforementioned one and the embarrassing REPL of js/ts, with the caveat being, this doesn't reproduce the real ts dev cycle. Still, one thing at a time, get good at the language, and then learn the tooling.