Remember the trigonometric addition identity

If you're like me, you don't remember trig identities. If you're like me, you prefer rederiving stuff yourself. It's a perk of math that we replace memorization with derivation. Still, it takes time, and distracts you from what you're actually doing. Also, deriving trig identities isn't so easy without some extra knowledge.

I once read this text about the use of proofs in mathematics. There was a quote from a math professor which went along the lines "it's a mnemonic device", and thats the point of this post. For a long time my inability to recall trig facts has been bugging me, until a day ago I skimmed "Trigonometry" by Gelfand and downloaded some knowledge into my brain. Turns out many identities can be derived just from the addition identity, so today we'll see two proofs, and hopefully you will be able to recall them in times of need.

Proof 1: Euler's identity

This one I think is the easiest to recall and deduce the identity from. The downside is it requires knowledge of complex numbers and Euler's identity

$$e^{i\theta}=\cos \theta +i\sin \theta$$

If you suffer an aneurism when seeing this move on to the next section. Otherwise, with this identity we can simply use exponent rules and multiplication to figure out the addition identities. First

$$e^{i(\alpha + \beta)}=e^{i\alpha}e^{i \beta}=(\cos \alpha +i\sin \alpha)(\cos \beta+i\sin \beta)$$

of course, the important part is to remember this quickly, so here's a nice visual aid

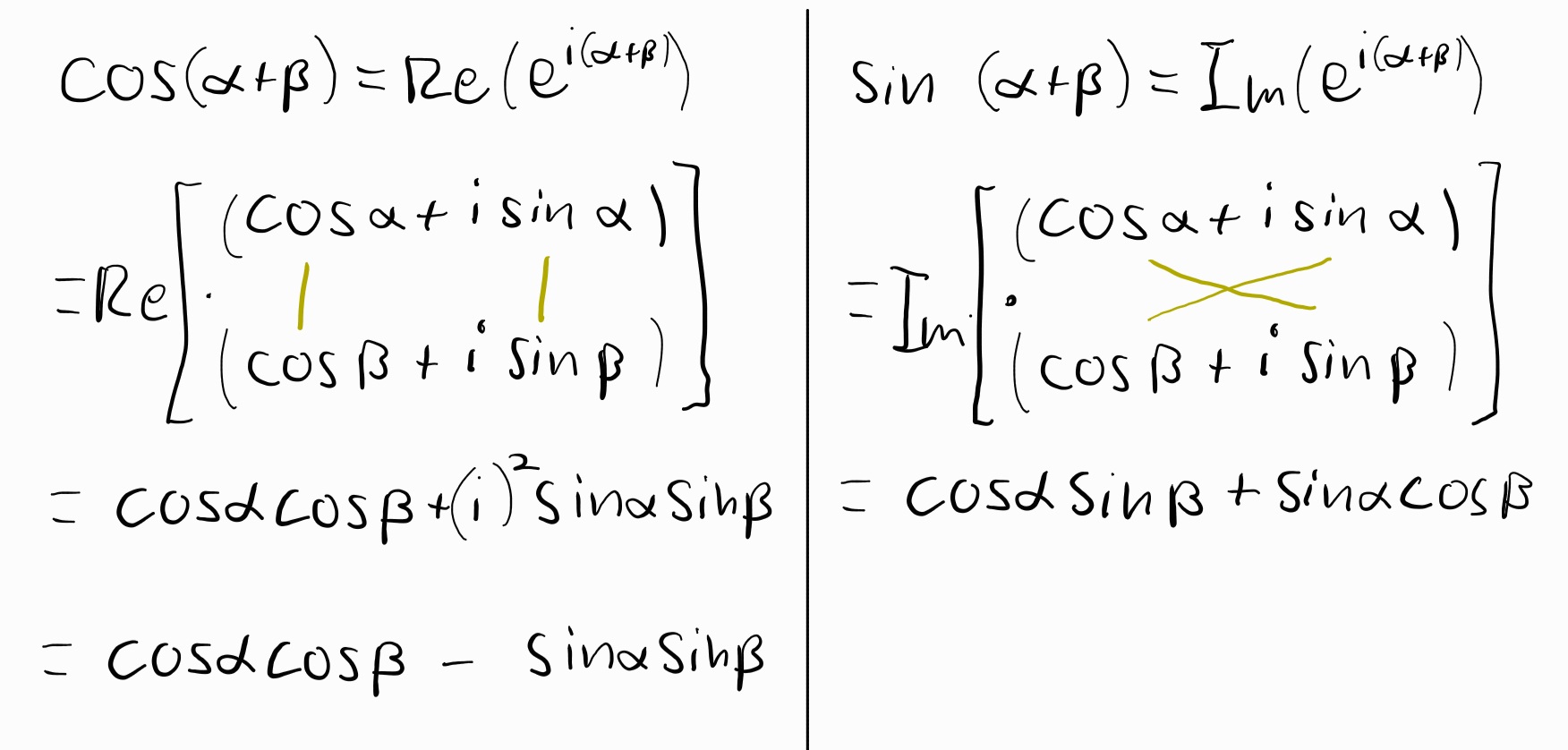
in a pinch, visualize this array and the colored lines.

Proof 2: Ptolemy

If you don't know Euler's identity, or you prefer something geometric, the next one may be for you. There are a couple of geometric proofs but I think this one might be cleaner for recall purposes. We will use the following characterization of sine: Let $\alpha$ be an angle in a circle of diameter $d$ as in the drawing. Then

$$\sin\alpha = \frac {PB}{d}$$

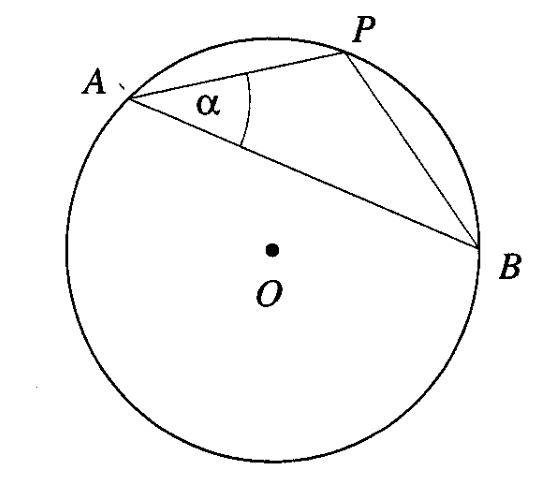
We use a construction as below in a circle of diameter 1.

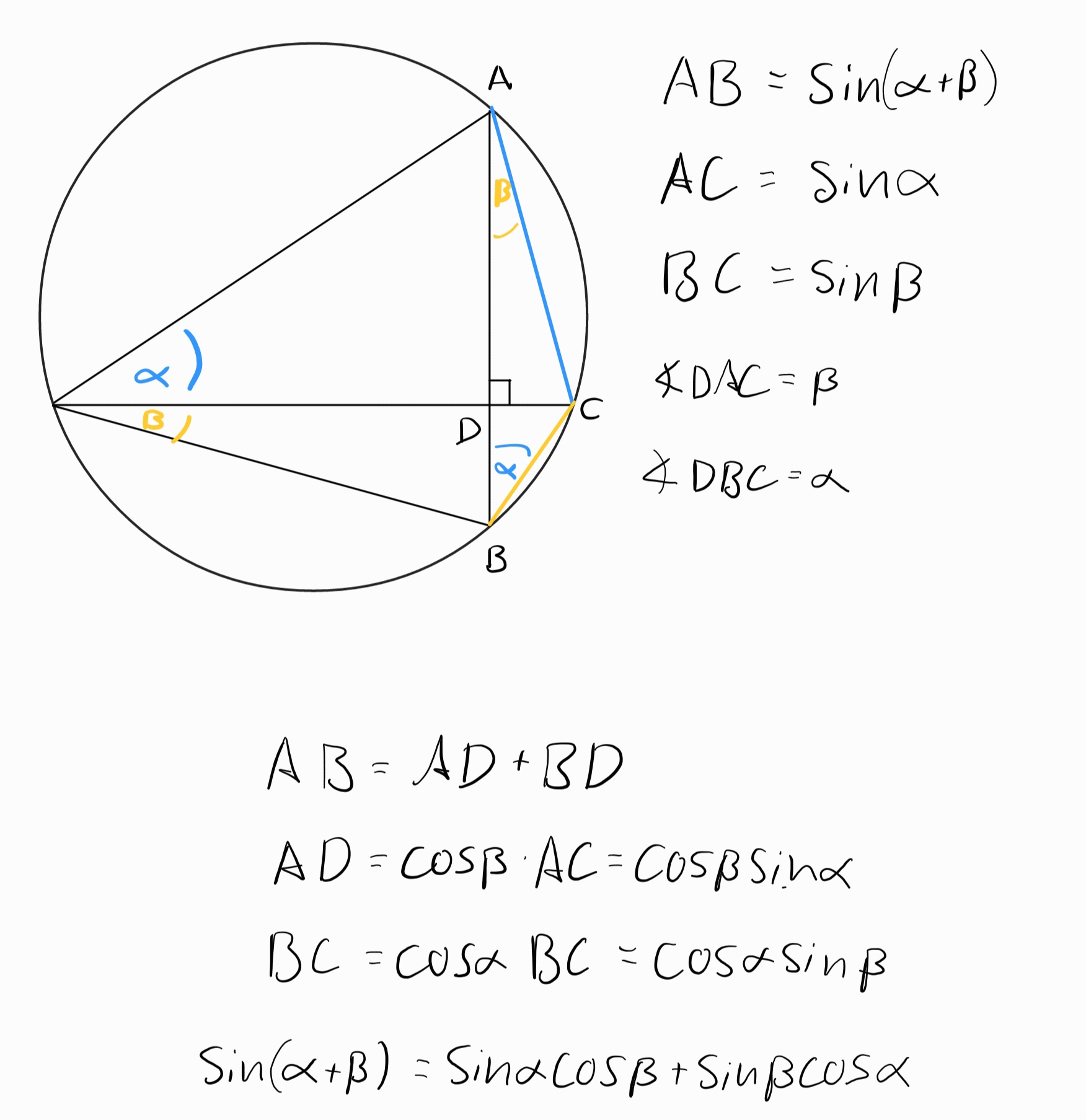
Deriving other identities

Using the addition identity you can quickly derive many other identities. Below are some, I suggest you try it yourself before looking at the answer.

cosine and sine of difference

We can just use $\cos -\alpha=\cos\alpha$ and $\sin-\alpha=-\sin\alpha$, so for example

$$ \sin(\alpha-\beta)=\sin(\alpha+(-\beta))=\sin\alpha\cos-\beta+\sin-\beta\cos\alpha=\sin\alpha\cos\beta-\sin\beta\cos\alpha $$

tangent of addition

Again, just use definition and addition identities

$$\tan(\alpha+\beta)=\frac{\sin(\alpha+\beta)}{\cos(\alpha+\beta)}=\frac{\sin\alpha\cos\beta+\sin\beta\cos\alpha}{\cos\alpha\cos\beta-\sin\alpha\sin\beta}=\frac{\frac{\sin\alpha}{\cos\alpha}+\frac{\sin\beta}{\cos\beta}}{1-\frac{\sin\alpha\sin\beta}{\cos\alpha\cos\beta}} = \frac{\tan \alpha +\tan \beta}{1-\tan \alpha +\tan \beta}$$

double angle

$$ \sin2\alpha = \sin(\alpha+\alpha)=2\sin\alpha\cos\alpha $$

multiplication of cosines and sines

This requires a tad more thinking, but based on the fact that a negative angle change sign only for sine we can turn multiplication to addition, for example

$$ \cos(\alpha+\beta)+\cos(\alpha-\beta)=2\cos\alpha\cos\beta-\sin\alpha\sin\beta+\sin\alpha\sin\beta=2\cos\alpha\cos\beta $$

Wrapping up

Once again, math proves its might. By remembering one piece of information we can deduce a whole lot more, and begone rote memorization!