On advice from my uncle I'm continuing to fallback on task difficulty with RNNs.

Unc's tips: - Swirch to generation task - Try residuals - Go deeper - Add projections - No dropout?

Let's recreate Karpathy's classic post and train a language model on tiny-shakespeare. We can get the entire dataset which is a text file

from fastdownload import FastDownload

fp = FastDownload().download("https://raw.githubusercontent.com/karpathy/char-rnn/master/data/tinyshakespeare/input.txt")
with open(fp) as f:
    data = f.read()
data[:100]
# 'First Citizen:\nBefore we proceed any further, hear me speak.\n\nAll:\nSpeak, speak.\n\nFirst Citizen:\nYou'

Using character-level tokenization, we simply index the set of characters in the text

vocab = list(set(data))
c2i = lambda c: vocab.index(c)
i2c = lambda i: vocab[i]
ds = torch.tensor([c2i(d) for d in data])

def decode(x):
    return "".join([i2c(i) for i in x])

The samples from the dataset will then be substrings of some fixed length. Here's a dataloader code

sample_inds = torch.randint(len(ds)-MAX_LEN, (bs,))
x = torch.stack([ds[i:i+MAX_LEN] for i in sample_inds])

Were starting with a straight-forward RNN model, using a GRU for the recurrence

class LM(nn.Module):
    def __init__(self, vocab_size, hidden_dim, num_layers=1):
        super(LM, self).__init__()
        self.embedding = nn.Embedding(vocab_size, hidden_dim)
        self.gru = nn.GRU(hidden_dim, hidden_dim, num_layers=num_layers, batch_first=True)
        self.linear = nn.Linear(hidden_dim, vocab_size)

    def forward(self, x):
        emb = self.embedding(x)
        out, h = self.gru(emb)
        out = self.linear(F.relu(out))
        out = F.log_softmax(out, dim=-1)
        return out

Questions we have for now: - do we need a non-linearity after the embedding? - is the log_softmax necessary?

On to the training loop

hidden_size = 512
num_layers = 1
lr = 2e-3
bs = 16
MAX_LEN = 40
epochs = 100000

lm = LM(len(vocab), hidden_size, num_layers).cuda()
opt = optim.Adam(lm.parameters(), lr)

progress_bar = tqdm(range(epochs)) 
display_handle = display(HTML("<div id='progress_output'></div>"), display_id=True)

for e in progress_bar:
    sample_inds = torch.randint(len(ds)-MAX_LEN-1, (bs,))
    sample = torch.stack([ds[i:i+MAX_LEN+1] for i in sample_inds]).cuda()
    x = sample[:,:-1]
    y = sample[:, 1:]

    lm.zero_grad()
    y_hat = lm(x)
    loss = F.cross_entropy(y_hat.view(-1, y_hat.size(-1)), y.flatten())
    loss.backward()
    opt.step()
    if e % 1000 == 0:
        y_pred = y_hat.topk(1, -1).indices
        progress_bar.set_postfix(loss=f"{loss:.2f}")
        update_info(display_handle, y_pred, y)

It's pretty standard: we feed in a batch of samples from the text, and use the out vector of each RNN iteration as the logprobs for the next token. We use the cross entropy loss. Here's a peek to the training

Up until now, the standard stuff, I'm already pretty good at it, but one would say this is the trivials. And once again, things don't look like they're converging. So from this point on, it's going to turn to more of a blocks of thoughts.

As a first step, let's try karpathy's hyperparameters. From the post

We can now afford to train a larger network, in this case lets try a 3-layer RNN with 512 hidden nodes on each layer.

Okay, so maybe I haven't been training for long enough? Other things to consider: gradient clipping?

First discovery: I noticed something interesting: if I reduce the hidden size to around 128 dims then I get 10x performance, and it seems to be a discontinuous jump.

I played around with the dataset size: dividing the dataset size by 5 let's the network get very low loss. But generation looks awful. The model's parameter count was 0.4 million, while the entire dataset consists of a million letters, so decreasing the dataset size gives as more parameters than characters. That might be some kind of memorization.

I played around with parameters for a while, got all kinds of different results, but nothing that looks like a clear win. Karpathy trained for a few hours. Maybe we should do the same? before that though, there was another suggestion from uncle: incorporate residual/skip connections. This is actually something that doesn't really appear in RNN tutorials, probably because ResNets and transformers appeared close to each other.

I decided to add skip connections between the outputs of each GRU layer, which forced me to write a bit more manual code

class LM(nn.Module):
    def __init__(self, vocab_size, embed_dim, hidden_dim, num_layers=1):
        super(LM, self).__init__()
        self.embedding = nn.Embedding(vocab_size, embed_dim)
        self.grus = [nn.GRU(embed_dim, hidden_dim, batch_first=True)] + [nn.GRU(hidden_dim, hidden_dim, batch_first=True) for i in range(1, num_layers)]
        self.grus = nn.ModuleList(self.grus)
        self.linear = nn.Linear(hidden_dim, vocab_size)


    def forward(self, x):
        emb = self.embedding(x)
        out, h = self.grus[0](emb)
        for gru in self.grus[1:]:
            out_hat, h = gru(out)
            out = out + out_hat
        out = self.linear(out)
        return out

Now I can increase the number of layers to 8 and get the loss down to 0.8, which still isn't great.

Okay, spent Saturday on this, I think it's enough. I'm gonna let stuff train, and hope the loss isn't stuck at 0.78 like it appears below

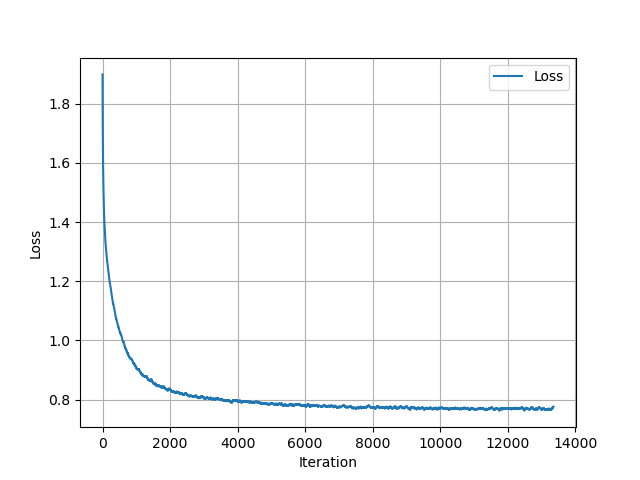
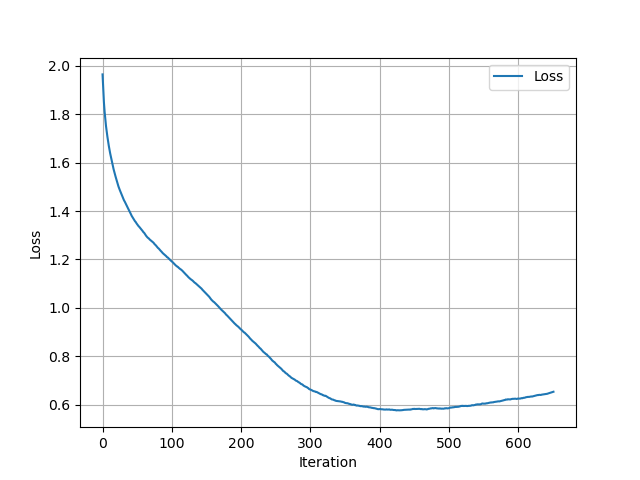
So afterwards I trained an 8-layer RNN and managed to get the loss down to below 0.6 for a while (although the net deteriorated afterwards)

but I still got things like

    

        Target:
        
our, my lord.

COMINIUS:
'Tis not a mile; briefly we heard their drums:
How couldst thou in a mile confound an hour,
And bring thy news so late?

Messenger:
Spies of the Volsces
Held me in chase, that
    
    

        Predicted:
        
au   my lord.

CORINIUS:
HTis not a pile- buiefly mi haard the r heym::
Haw fauldst thou sn m mill aoafound an hour,
Ynd bling thy news wo late?

Messenger:
Spies of the Volsces
Hald me in chase, that
    

seemingly many misspellings etc. But then I realized, no, I'm being stupid, it's the visualization that's misleading. You can't compare the target vs predicted, because the model will always make mistakes! it can't 100% guess the first letter of a new word without memorization for example. What we really want to see is generation. So here I present to you my model's creation

If he did not care whether he had their love or no, henge him: Though inducedly lord hath cloudy nothing cursed With lasting Richard see'st, is a noble

And it's great! a better visualization is to color each wrongly predicted letter, like below

    

        Colored Target:
        
e way
To call hers exquisite, in question more:
These happy masks that kiss fair ladies' brows
Being black put us in mind they hide the fair;
He that is strucken blind cannot forget
The precious treas
    

We can see that the biggest mistakes are when there is a lot of uncertainty on the next letter which is natural. In fact, I by the lack of mistakes here I suspect it might already be memorizing the dataset.

What's the lesson here? making mistakes is part of the process, Show your work, and have fun! I do wonder though how many of my previous puzzled moments were caused by this confusion. Still, for now, we have a first victory.

Link to notebook